Analyse • IA, IA, mais qui es-tu donc ?

Et maintenant ?

En résumé, le perceptron est bien chouette, mais il faut atteindre un certain nombre de neurones pour réussir à obtenir des résultats convaincants, ce qui n’est pas chose facile lorsque les capacités de calcul sont limitées. Ainsi, c’est dans la fin des années 2000 et les années 2010 que le machine learning prend son envol, aidé par des architectures matérielles et des frameworks logiciels permettant enfin d’exploiter le potentiel des réseaux, tout en laissant libre cours à l’expérimentation de certains. Après avoir posé un cadre théorique, la recherche empirique de topologies (c’est-à-dire du moyen le meilleur d’agencer les couches [connexions, nombre de neurones]) a pu prendre son envol.

Il faut changer sa couche !

CNN : Viva la convoluzion

Empiler des couches type perceptron les unes sur les autres formes ce que l’on nomme des couches denses : tous les neurones d’une couche sont reliés à tous les neurones de la couche suivante. Si cela est pertinent dans des tâches où la place des données n’apporte pas d’information (par exemple pour croiser des statistiques entres elles de manière brutale), cela n’est pas le plus adapté pour les autres situations. Pour les applications de traitement d’image, typiquement, les pixels situés à l’autre bout du fichier ont peu de chance d’indiquer des informations pertinentes. En revanche, les pixels voisins, eux, permettent de détecter des formes, nuances et autres dégradés : bref, des éléments plus intéressants. Ainsi, un nouveau type de couche a rapidement pris le pas sur ces applications : les CNN, ou Convolutionnal Neural Networks. Leur fonctionnement est similaire au perceptron, si ce n’est que les neurones ne voient qu’une fenêtre de l’image d’entrée (par exemple un carré de 5x5 px ou 9x9 px). Notez qu’une image, sur ordinateur, possède une dimension de plus que sa longueur et sa largeur : les canaux, initialement les trois couleurs rouge, vert et bleu de l’image. Dans un CNN, ces canaux sont traités indifféremment par un CNN (connexions complètes) et sont convertis en un nombre plus important de fonctionnalités [features]). Un CNN typique va ainsi augmenter le nombre de fonctionnalités et diminuer la taille spatiale pour extraire des informations, avant de condenser le tout au moyen de couches complètes que l’on nomme tête du réseau.

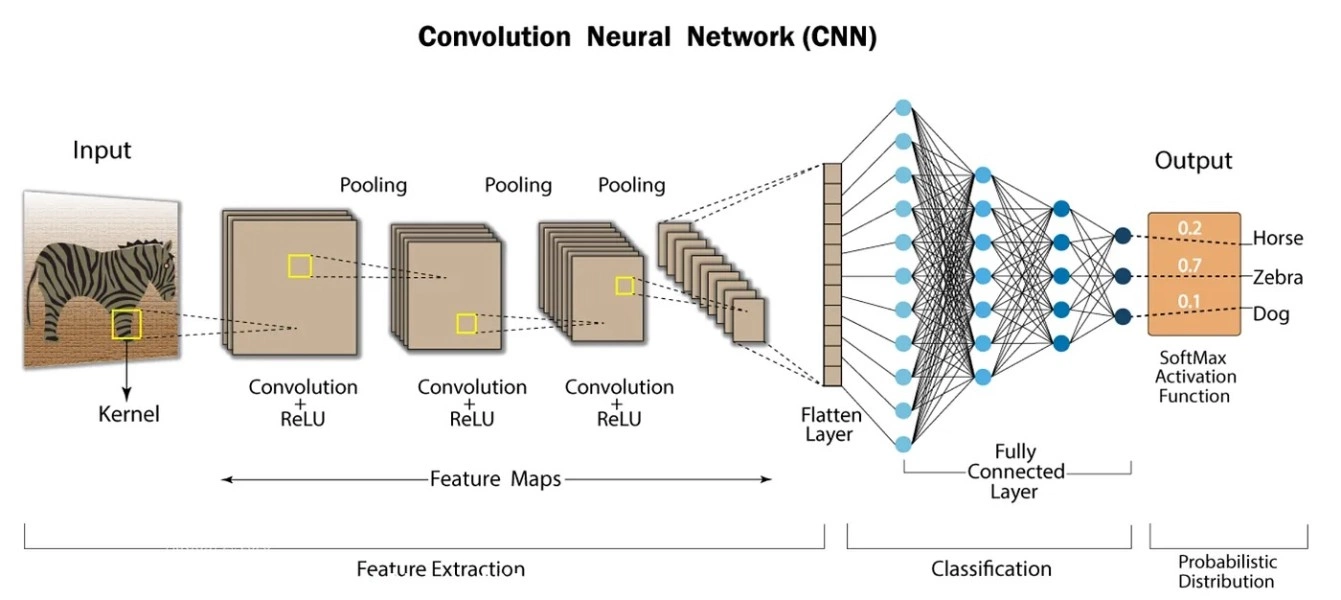
La structure typique d’un CNN « simple ». Les premières couches de convolutions extraient les « features » en réduisant la taille spatiale de l’image au profit des fonctionnalités (épaisseur des images sur le schéma). Puis, le tout est converti en un vecteur, qui perd toute l’information spatiale. Enfin, la tête (couche de classification) permet d’obtenir en sortie la probabilité (pourcentage de chance d’après le réseau) que l’image contienne un cheval, un zèbre, un chien, etc. (Crédit : LinkedIn)

De ce fait, les couches convolutionnelles, proche de l’image, apprendront des motifs basiques (cercles, lignes, vagues,…), là où les couches intermédiaires combineront ces informations pour reconnaître des structures combinant plusieurs motifs (main, visage, corps,…). Enfin, la tête du réseau ne sert qu’à classifier ces informations, par exemple en reconnaissant un chat, un humain, un chien. Il est ainsi monnaie courante de remplacer la tête d’un réseau déjà entraîné par une nouvelle tête afin de réentrainer le bouzin pour une nouvelle tâche : un réseau reconnaissant un animal peut ainsi être utilisé pour classer des fleurs, et ce à moindre temps/coût (nous y reviendront dans deux pages). Au passage, ce phénomène de plasticité cérébrale n’est pas sans rappeler le même phénomène chez l’homme : comme quoi, ces réseaux artificiels ne sont pas si loin de leurs homologues biologiques.

RNN, LSTM : tout est une histoire de mémoire

De même, les réseaux de neurones sont également impliqués dans des tâches de traitement audio et vidéo, cas dans lequel les données possèdent une dimension temporelle. Dans le même esprit que les CNN, les couches denses sont moins efficaces et difficilement entraînables, car elles mettent au même niveau les mots situés au début et à la fin de la phrase, ce qui ne correspond pas aux grammaires des langues humaines, qui reposent sur le contexte. Dans ce cas, ce sont des réseaux dits récurrents (ou RNN) qui sont à l’œuvre. Ils possèdent un lien reliant chaque neurone à lui-même pour lui rappeler la valeur précédente donnée en sortie, d’où le qualificatif de « récurrents » ; lien que l’on peut également interpréter comme la présence d’une mémoire au sein du réseau, ou encore comme un réseau bien plus grand dont les neurones partagent leur poids/biais — si vous avez oublié de quoi il s’agit… direction la page précédente !

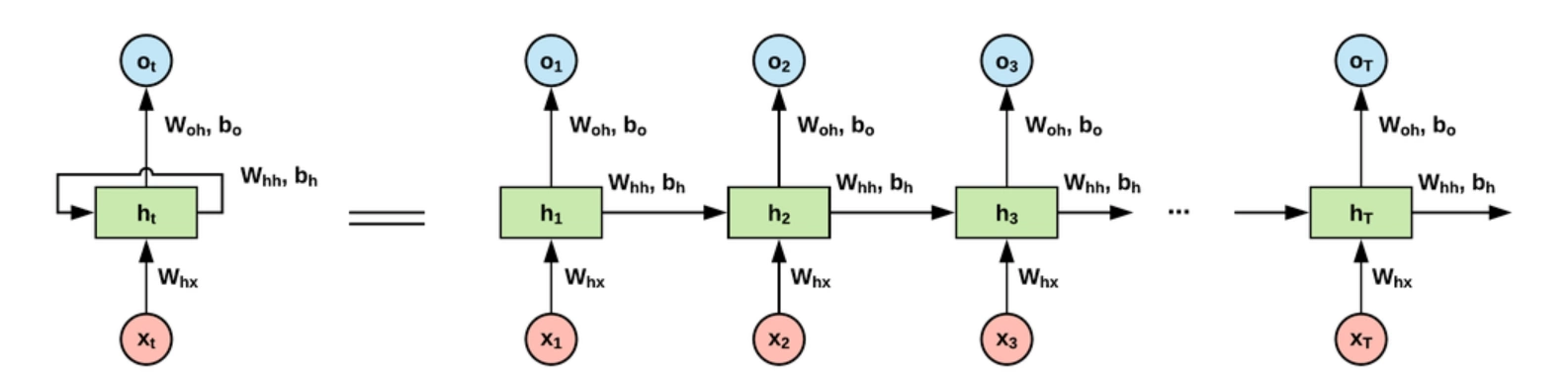
Un seul neurone récurrent (à gauche), avec sa liaison récurrente. De l’autre côté du signe « = », son interprétation déroulée : une succession de neurones partageant le même poids (w_oh) et biais (b_o). En revanche, la sortie du neurone précédent (contrôlée par w_hh et b_h) est connectée à l’entrée du neurone suivant, tout comme la nouvelle donnée d’entrée (contrôlée, elle, par w_hx).

Les LSTM (Long Short-Term Memory) poussent le concept plus loin encore en contrôlant la quantité de données issues de l’itération précédente en les stockant dans une cellule. Cette dernière est mise à jour et utilisée en fonction de valeurs prises par un signal d’entrée (input gate), un signal de sortie (exit gate) et une porte d’oublie (reset gate). Là encore, ce sont des coefficients similaires aux poids du perceptron qui régissent ces flots, avec l’avantage de permettre un entraînement de ces derniers plus aisé, pour ceux qui ont le courage de se plonger dans les mathématiques cachées dernières ces structures — à savoir, par nous ! —, car la cellule permet de conserver des informations au travers des couches, rendant les mécanismes de corrections des poids (voir page 6 pour plus de détails !) plus efficaces. Cependant, du fait du nombre considérable de coefficients à étalonner, les LSTM se font peu à peu délaisser au profit des GRU (Gated recurrent units), qui reprenne le principe en retirant le signal de sortie. Là encore, l’idée est de pouvoir en caser davantage pour la même puissance de calcul, et pouvoir entraîner le bouzin plus simplement.

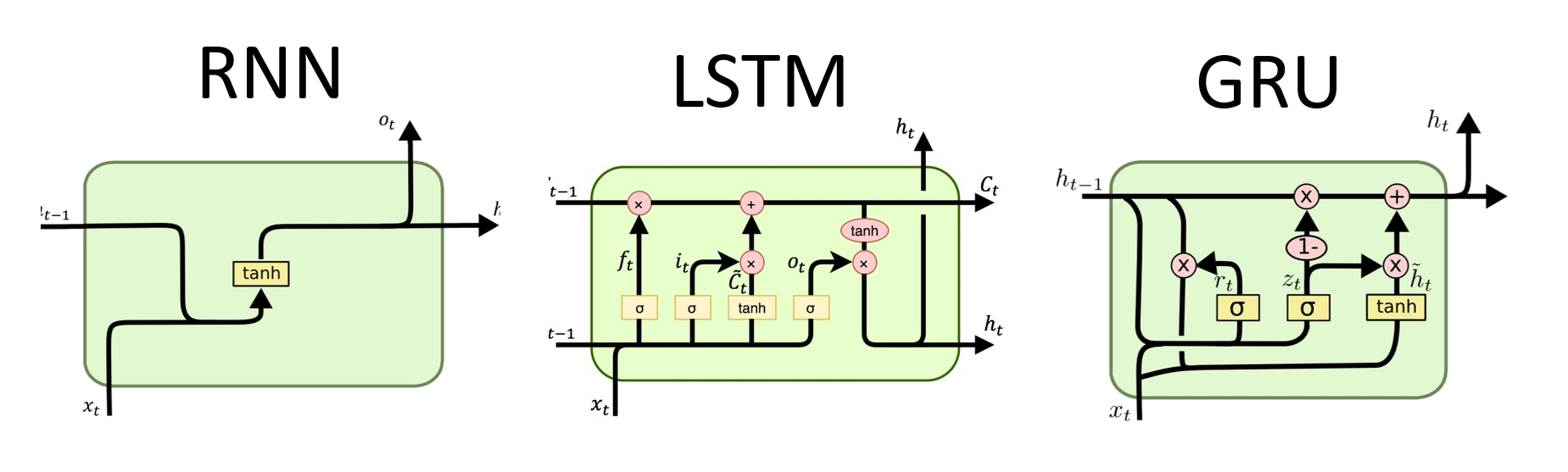
Bon, clairement, là, on ne va pas trop rentrer dans les détails. Les flèches provenant du bas représentent les informations de la couche inférieure, et celle du haut, les informations qui vont vers couche supérieure. Côté gauche, h_t-1 correspond à la sortie du neurone au pas de temps précédent, et à droite, la flèche envoie h_t au pas de temps suivant à d’autres neurones.

Sans trop rentrer dans les détails, le RNN est très (trop) simpliste pour retenir efficacement de l’information. Le LSTM, lui, est bien plus complexe, mais paye le prix avec trois σ (traitement des signaux). Sur le GRU, seul deux σ sont nécessaires : la complexité est réduite !

Aparté : les réseaux creux

Toutes les couches abordées dans cette section ont un point commun : elles prennent en entrée toutes les données de la couche précédente, pour donner une sortie complète. En même temps, que faire d’autre ? Hé bien, il est possible de faire des réseaux dit creux (ou sparse en anglais) en prenant un réseau classique (dit dense) et en retirant une partie des neurones, typiquement ceux associés aux poids les plus faibles. Cette technique se base sur l’hypothèse du ticket gagnant qui suppose que dans tout réseau dense, il existe un sous-réseau creux de précision similaire (l’analogie avec le loto est claire : parmi tous les tickets, il en existe un gagnant). Pour passer d’un réseau dense à un réseau creux, il suffit de fixer à zéro les valeurs des poids/biais que l’on souhaite retirer, et, souvent, réentraîner le bousin en forçant ces zéros, histoire de récupérer un peu de la précision perdue.

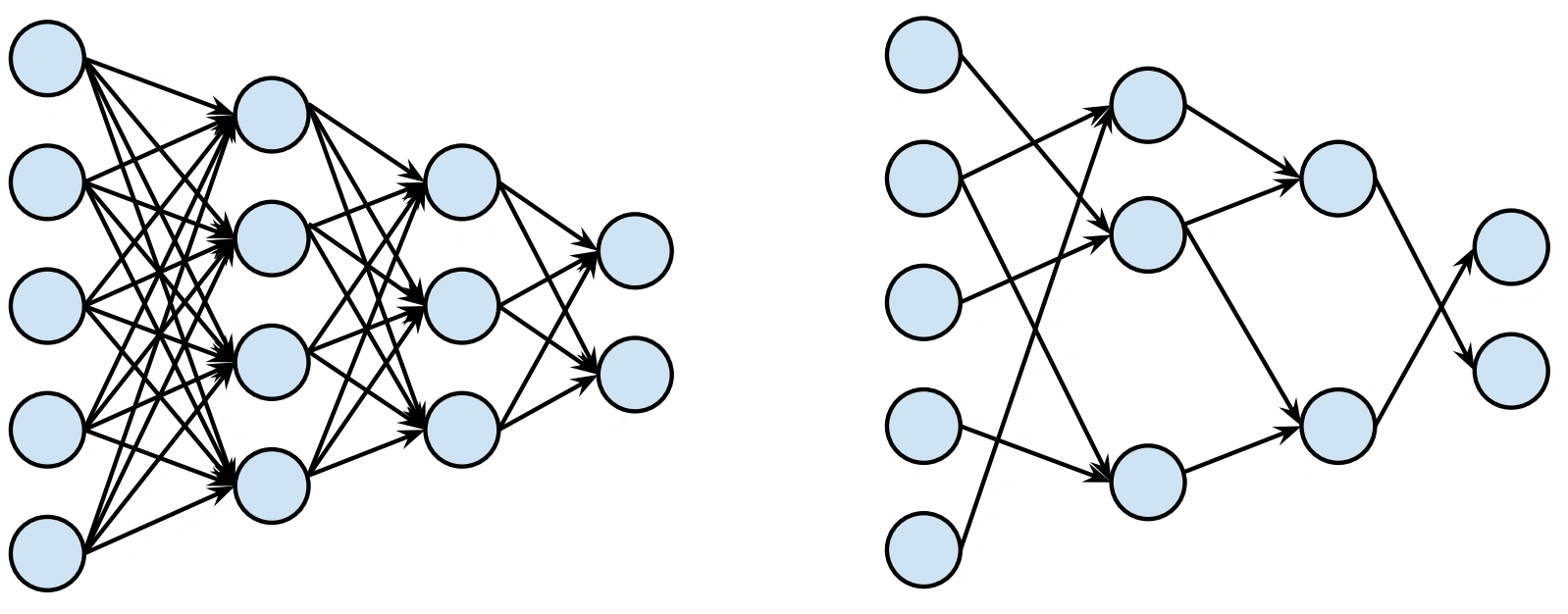
À gauche, un réseau dense. À droite, la version creuse, retirant à la fois des neurones, mais aussi des poids (flèches).

L’intérêt de tout ça ? Économiser en puissance de calcul, pardi ! Si le même résultat peut être atteint avec moitié moins de neurones, alors il suffit de moitié moins de calcul : pratique pour l’embarqué, ou pour les fermes de GPU dont le but est d’effectuer en masse de l’inférence. Dans la pratique, les produits matriciels nécessaires à l’inférence passent ainsi de denses à creux, ce qui peut s’encoder de deux manières différentes : soit en représentant explicitement les zéros (i.e. en gardant le même encodage que pour une matrice dense, ce qui n’est pas très efficace en matière de stockage), soit en ne stockant que les nombres différents de zéros dans un format dit compressé, typiquement CSR ou CSC. Or, au passage, les jolis accès séquentiels deviennent aléatoires : au lieu d’avoir les poids et biais des neurones côte à côte, la sparsité engendre des « trous » imprévisibles dans les accès mémoires… ce qui n’est pas du plus simple pour le hardware !

Devinez quoi ? Cet inventaire est (très) loin d’être complet. Il existe de nombreux autres types de couches permettant par exemple de réduire la taille des données (pooling) ou de l’augmenter (transposed convolution), et les fonctions d’activations qui leur font suites sont, elles aussi, des objets d’étude à part entière !

C’en est (enfin) bon pour cette typologie des neurones, rendez-vous page suivante pour voir comment ces derniers sont rassemblés au sein de réseaux performants… et bien plus encore !